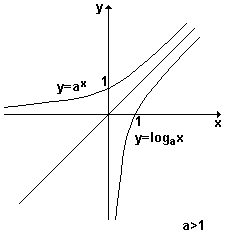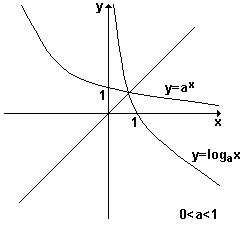9.21.2010
Função exponencial
A função exponencial
A função exponencial natural é a função exp:R®R+, definida como a inversa da função logarítmo natural, isto é:
Ln[exp(x)]=x, exp[Ln(x)]=x
O gráfico da função exponencial é obtido pela reflexão do gráfico da função Logaritmo natural em relação à identidade dada pela reta y=x.
Como o domínio da função Logaritmo natural é o conjunto dos números reais positivos, então a imagem da função exp é o conjunto dos números reais positivos e como a imagem de Ln é o conjunto R de todos os números reais, então o domínio de exp também é o conjunto R de todos os números reais.
Observação: Através do gráfico de f(x)=exp(x), observamos que:
1. exp(x)>0 se x é real)
2. 0<1 se x<0
3. exp(x)=1 se x=0
4. exp(x)>1 se x>0
No Ensino Médio, a função exponencial é definida a partir da função logarítmica e ciclicamente define-se a função logarítmica em função da exponencial como:
f(x)=exp(x), se e somente se, x=Ln(y)
Para uma definição mais cuidadosa, veja Logaritmos.
Exemplos:
A Constante e de Euler
Existe uma importantíssima constante matemática definida por
e = exp(1)
O número e é um número irracional e positivo e em função da definição da função exponencial, temos que:
Ln(e)=1
Este número é denotado por e em homenagem ao matemático suíço Leonhard Euler (1707-1783), um dos primeiros a estudar as propriedades desse número.
O valor deste número expresso com 40 dígitos decimais, é:
e=2,718281828459045235360287471352662497757
Conexão entre o número e e a função exponencial
Se x é um número real, a função exponencial exp(.) pode ser escrita como a potência de base e com expoente x, isto é:
ex = exp(x)
Significado geométrico de e
Tomando um ponto v do eixo OX, com v>1 tal que a área da região do primeiro quadrante localizada sob a curva y=1/x e entre as retas x=1 e x=v seja unitária, então o valor de v será igual a e.
Propriedades básicas da função exponencial
Se x e y são números reais e k é um número racional, então:
Simplificações matemáticas
Podemos simplificar algumas expressões matemáticas com as propriedades das funções exponenciais e logaritmos:
Outras funções exponenciais
Podemos definir outras funções exponenciais como g(x)=ax, onde a é um número real positivo diferente de 1 e de x. Primeiro, consideremos o caso onde o expoente é um número racional r.
Tomando x=ar na equação x=exp[Ln(x)], obtemos:
ar=exp[Ln(ar)]
Como Ln[ar]=r.Ln(a), a relação acima fica na forma:
ar = exp[r.Ln(a)]
Esta última expressão, juntamente com a informação que todo número real pode ser escrito como limite de uma sequência de números racionais, justifica a definição para g(x)=ax, onde x é um número real:
ax=exp[x.Ln(a)]
Leis dos expoentes
Se x e y são números reais, a e b são números reais positivos, então:
Se i é a unidade imaginária e x é um número real, então vale a relação:
eix = exp(ix) = cos(x) + i sen(x)
Algumas Aplicações
Funções exponenciais desempenham papéis fundamentais na Matemática e nas ciências envolvidas com ela, como: Física, Química, Engenharia, Astronomia, Economia, Biologia, Psicologia e outras. Vamos apresentar alguns exemplos com aplicações destas funções.
Lei do resfriamento dos corpos: Um indivíduo foi encontrado morto em uma sala com temperatura ambiente constante. O legista tomou a temperatura do corpo às 21:00 h e constatou que a mesma era de 32 graus Celsius. Uma hora depois voltou ao local e tomou novamente a temperatura do corpo e constatou que a mesma estava a 30 graus Celsius. Aproximadamente a que horas morreu o indivíduo, sabendo-se que a temperatura média de um corpo humano normal é de 37 graus Celsius?
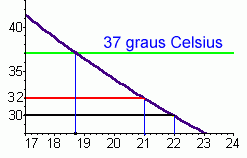
Partindo de estudos matemáticos pode-se construir uma função exponencial decrescente que passa pelos pontos (21,32) e (22,30) onde abscissas representam o tempo e as ordenadas a temperatura do corpo.
A curva que descreve este fenômeno é uma função exponencial da forma:
f(t) = C eA t
então obtemos que:
A = Ln(30)-Ln(32)
C = 32/ (30/32)21
A função exponencial que rege este fenômeno de resfriamento deste corpo é dada por:
f(t) = 124,09468 e-0,0645385t
e quando f(t) = 37 temos que:
t = 18,7504... = 18 horas + 45 minutos
que pode ser observado através do gráfico.
Observação: Neste exemplo, usamos a construção de um gráfico e as propriedades operatórias das funções exponenciais e logarítmicas.
Curvas de aprendizagem: Devido ao seu uso por psicólogos e educadores na descrição do processo de aprendizagem, as curvas exponenciais realizam um papel importante.
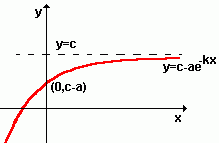
A curva básica para este tipo de estudo é da forma:
f(x) = c - a e-k.x
onde c, a e k são constantes positivas. Considerando o caso especial em que c=a temos uma das equações básicas para descrever a relação entre a consolidação da aprendizagem y=f(x) e o número de reforços x.
A função:
f(x) = c - a e-k.x
cresce rapidamente no começo, nivela-se e então aproxima-se de sua assíntota y=c.
Estas curvas também são estudadas em Economia, na representação de várias funções de custo e produção.
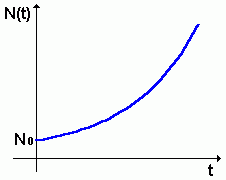
Crescimento populacional: Em 1798, Thomas Malthus, no trabalho "An Essay on the Principle of Population" formulou um modelo para descrever a população presente em um ambiente em função do tempo. Considerou N=N(t) o número de indivíduos em certa população no instante t. Tomou as hipóteses que os nascimentos e mortes naquele ambiente eram proporcionais à população presente e a variação do tempo conhecida entre os dois períodos. Chegou à seguinte equação para descrever a população presente em um instante t:
N(t)=No ert
onde No é a população presente no instante inicial t=0 e r é uma constante que varia com a espécie de população.
O gráfico correto desta função depende dos valores de No e de r. Mas sendo uma função exponencial, a forma do gráfico será semelhante ao da função y=Kex.
Este modelo supõe que o meio ambiente tenha pouca ou nenhuma influência sobre a população.
Desse modo, ele é mais um indicador do potencial de sobrevivência e de crescimento de cada espécie de população do que um modelo que mostre o que realmente ocorre.
Consideremos por exemplo uma população de bactérias em um certo ambiente. De acordo com esta equação se esta população duplicar a cada 20 minutos, dentro de dois dias, estaria formando uma camada em volta da terra de 30 cm de espessura. Assim, enquanto os efeitos do meio ambiente são nulos, a população obedece ao modelo N=Noert. Na realidade, se N=N(t) aumenta, o meio ambiente oferece resistência ao seu crescimento e tende a mantê-lo sobre controle. Exemplos destes fatores são, a quantidade disponível de alimentos, acidentes, guerras, epidemias,...
Como aplicação numérica, consideremos uma colônia de bactérias se reproduzindo normalmente. Se num certo instante havia 200 bactérias na colônia, passadas 12 horas havia 600 bactérias. Quantas bactérias haverá na colônia após 36 horas da última contagem?
No instante inicial havia 200 bactérias, então No=200, após 12 horas havia 600 bactérias, então
N(12)=600=200 er12
logo
e12r=600/200=3
assim
ln(e12r)=ln(3)
Como Ln e exp são funções inversas uma da outra, segue que 12r=ln(3), assim:
r=ln(3)/12=0,0915510
Finalmente:
N(48) = 200 e48.(0,0915510) = 16200 bactérias
Então, após 36 horas da útima contagem ou seja, 48 horas do início da contagem, haverá 16200 bactérias.
Desintegração radioativa: Os fundamentos do estudo da radioatividade ocorrerram no início do século por Rutherford e outros. Alguns átomos são naturalmente instáveis, de tal modo que após algum tempo, sem qualquer influência externa sofrem transições para um átomo de um novo elemento químico e durante esta transição eles emitem radiações. Rutherford formulou um modelo para descrever o modo no qual a radioatividade decai. Se N=N(t) representa o número de átomos da substância radioativa no instante t, No o número de átomos no instante t=0 e k é uma constante positiva chamada de constante de decaimento, então:
N(t) = No e-k.t
esta constante de decaimento k, tem valores diferentes para substâncias diferentes, constantes que são obtidas experimentalmente.
Na prática usamos uma outra constante T, denominada meia-vida do elemento químico, que é o tempo necessário para que a quantidade de átomos da substância decaia pela metade.
Se N=No/2 para t=T, temos
No/2 = No e-k.T
assim
T=Ln(2)/k
Na tabela, apresentamos indicadores de meia-vida de alguns elementos químicos:
Para o Carbono 14, a constante de decaimento é:
k = Ln(2)/T = Ln(2)/5568 = 12,3386 por ano
Fonte: AlgoSobre
A função exponencial natural é a função exp:R®R+, definida como a inversa da função logarítmo natural, isto é:
Ln[exp(x)]=x, exp[Ln(x)]=x
O gráfico da função exponencial é obtido pela reflexão do gráfico da função Logaritmo natural em relação à identidade dada pela reta y=x.
Como o domínio da função Logaritmo natural é o conjunto dos números reais positivos, então a imagem da função exp é o conjunto dos números reais positivos e como a imagem de Ln é o conjunto R de todos os números reais, então o domínio de exp também é o conjunto R de todos os números reais.
Observação: Através do gráfico de f(x)=exp(x), observamos que:
1. exp(x)>0 se x é real)
2. 0
3. exp(x)=1 se x=0
4. exp(x)>1 se x>0
No Ensino Médio, a função exponencial é definida a partir da função logarítmica e ciclicamente define-se a função logarítmica em função da exponencial como:
f(x)=exp(x), se e somente se, x=Ln(y)
Para uma definição mais cuidadosa, veja Logaritmos.
Exemplos:
- Ln[exp(5)]=5
- exp[ln(5)]=5
- Ln[exp(x+1)1/2]=(x+1)1/2
- exp[Ln((x+1)1/2]=(x+1)1/2
- exp[3.Ln(x)]=exp(Ln(x³)]=x³
- exp[k.Ln(x)]=exp[Ln(xk)]=xk
- xp[(7(Ln(3)-Ln(4)]=exp[7(Ln(3/4))]=exp[(Ln(3/4)]7)=(3/4)7
A Constante e de Euler
Existe uma importantíssima constante matemática definida por
e = exp(1)
O número e é um número irracional e positivo e em função da definição da função exponencial, temos que:
Ln(e)=1
Este número é denotado por e em homenagem ao matemático suíço Leonhard Euler (1707-1783), um dos primeiros a estudar as propriedades desse número.
O valor deste número expresso com 40 dígitos decimais, é:
e=2,718281828459045235360287471352662497757
Conexão entre o número e e a função exponencial
Se x é um número real, a função exponencial exp(.) pode ser escrita como a potência de base e com expoente x, isto é:
ex = exp(x)
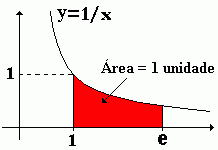
Significado geométrico de e
Tomando um ponto v do eixo OX, com v>1 tal que a área da região do primeiro quadrante localizada sob a curva y=1/x e entre as retas x=1 e x=v seja unitária, então o valor de v será igual a e.
Propriedades básicas da função exponencial
Se x e y são números reais e k é um número racional, então:
- y=exp(x) se, e somente se, x=Ln(y).
- exp[Ln(y)]=y para todo y>0.
- Ln[exp(x)]=x para todo x real.
- exp(x+y)=exp(x) exp(y)
- exp(x-y)=exp(x)/exp(y)
- exp(x.k)=[exp(x)]k
Simplificações matemáticas
Podemos simplificar algumas expressões matemáticas com as propriedades das funções exponenciais e logaritmos:
- exp[Ln(3)]=3.
- Ln[exp(20x)]=20x.
- exp[5.Ln(2)]=exp[Ln(25)]=25=32.
- exp[2+5.ln(2)]=exp(2)exp(5.Ln(2))=32e².
Outras funções exponenciais
Podemos definir outras funções exponenciais como g(x)=ax, onde a é um número real positivo diferente de 1 e de x. Primeiro, consideremos o caso onde o expoente é um número racional r.
Tomando x=ar na equação x=exp[Ln(x)], obtemos:
ar=exp[Ln(ar)]
Como Ln[ar]=r.Ln(a), a relação acima fica na forma:
ar = exp[r.Ln(a)]
Esta última expressão, juntamente com a informação que todo número real pode ser escrito como limite de uma sequência de números racionais, justifica a definição para g(x)=ax, onde x é um número real:
ax=exp[x.Ln(a)]
Leis dos expoentes
Se x e y são números reais, a e b são números reais positivos, então:
- axay=ax+y
- ax/ay=ax-y
- (ax) y=ax.y
- (a b)x=axbx
- (a/b)x=ax/bx
- a-x=1/ax
Se i é a unidade imaginária e x é um número real, então vale a relação:
eix = exp(ix) = cos(x) + i sen(x)
Algumas Aplicações
Funções exponenciais desempenham papéis fundamentais na Matemática e nas ciências envolvidas com ela, como: Física, Química, Engenharia, Astronomia, Economia, Biologia, Psicologia e outras. Vamos apresentar alguns exemplos com aplicações destas funções.
Lei do resfriamento dos corpos: Um indivíduo foi encontrado morto em uma sala com temperatura ambiente constante. O legista tomou a temperatura do corpo às 21:00 h e constatou que a mesma era de 32 graus Celsius. Uma hora depois voltou ao local e tomou novamente a temperatura do corpo e constatou que a mesma estava a 30 graus Celsius. Aproximadamente a que horas morreu o indivíduo, sabendo-se que a temperatura média de um corpo humano normal é de 37 graus Celsius?
Partindo de estudos matemáticos pode-se construir uma função exponencial decrescente que passa pelos pontos (21,32) e (22,30) onde abscissas representam o tempo e as ordenadas a temperatura do corpo.
A curva que descreve este fenômeno é uma função exponencial da forma:
f(t) = C eA t
então obtemos que:
A = Ln(30)-Ln(32)
C = 32/ (30/32)21
A função exponencial que rege este fenômeno de resfriamento deste corpo é dada por:
f(t) = 124,09468 e-0,0645385t
e quando f(t) = 37 temos que:
t = 18,7504... = 18 horas + 45 minutos
que pode ser observado através do gráfico.
Observação: Neste exemplo, usamos a construção de um gráfico e as propriedades operatórias das funções exponenciais e logarítmicas.
Curvas de aprendizagem: Devido ao seu uso por psicólogos e educadores na descrição do processo de aprendizagem, as curvas exponenciais realizam um papel importante.
A curva básica para este tipo de estudo é da forma:
f(x) = c - a e-k.x
onde c, a e k são constantes positivas. Considerando o caso especial em que c=a temos uma das equações básicas para descrever a relação entre a consolidação da aprendizagem y=f(x) e o número de reforços x.
A função:
f(x) = c - a e-k.x
cresce rapidamente no começo, nivela-se e então aproxima-se de sua assíntota y=c.
Estas curvas também são estudadas em Economia, na representação de várias funções de custo e produção.
Crescimento populacional: Em 1798, Thomas Malthus, no trabalho "An Essay on the Principle of Population" formulou um modelo para descrever a população presente em um ambiente em função do tempo. Considerou N=N(t) o número de indivíduos em certa população no instante t. Tomou as hipóteses que os nascimentos e mortes naquele ambiente eram proporcionais à população presente e a variação do tempo conhecida entre os dois períodos. Chegou à seguinte equação para descrever a população presente em um instante t:
N(t)=No ert
onde No é a população presente no instante inicial t=0 e r é uma constante que varia com a espécie de população.
O gráfico correto desta função depende dos valores de No e de r. Mas sendo uma função exponencial, a forma do gráfico será semelhante ao da função y=Kex.
Este modelo supõe que o meio ambiente tenha pouca ou nenhuma influência sobre a população.
Desse modo, ele é mais um indicador do potencial de sobrevivência e de crescimento de cada espécie de população do que um modelo que mostre o que realmente ocorre.
Consideremos por exemplo uma população de bactérias em um certo ambiente. De acordo com esta equação se esta população duplicar a cada 20 minutos, dentro de dois dias, estaria formando uma camada em volta da terra de 30 cm de espessura. Assim, enquanto os efeitos do meio ambiente são nulos, a população obedece ao modelo N=Noert. Na realidade, se N=N(t) aumenta, o meio ambiente oferece resistência ao seu crescimento e tende a mantê-lo sobre controle. Exemplos destes fatores são, a quantidade disponível de alimentos, acidentes, guerras, epidemias,...
Como aplicação numérica, consideremos uma colônia de bactérias se reproduzindo normalmente. Se num certo instante havia 200 bactérias na colônia, passadas 12 horas havia 600 bactérias. Quantas bactérias haverá na colônia após 36 horas da última contagem?
No instante inicial havia 200 bactérias, então No=200, após 12 horas havia 600 bactérias, então
N(12)=600=200 er12
logo
e12r=600/200=3
assim
ln(e12r)=ln(3)
Como Ln e exp são funções inversas uma da outra, segue que 12r=ln(3), assim:
r=ln(3)/12=0,0915510
Finalmente:
N(48) = 200 e48.(0,0915510) = 16200 bactérias
Então, após 36 horas da útima contagem ou seja, 48 horas do início da contagem, haverá 16200 bactérias.
Desintegração radioativa: Os fundamentos do estudo da radioatividade ocorrerram no início do século por Rutherford e outros. Alguns átomos são naturalmente instáveis, de tal modo que após algum tempo, sem qualquer influência externa sofrem transições para um átomo de um novo elemento químico e durante esta transição eles emitem radiações. Rutherford formulou um modelo para descrever o modo no qual a radioatividade decai. Se N=N(t) representa o número de átomos da substância radioativa no instante t, No o número de átomos no instante t=0 e k é uma constante positiva chamada de constante de decaimento, então:
N(t) = No e-k.t
esta constante de decaimento k, tem valores diferentes para substâncias diferentes, constantes que são obtidas experimentalmente.
Na prática usamos uma outra constante T, denominada meia-vida do elemento químico, que é o tempo necessário para que a quantidade de átomos da substância decaia pela metade.
Se N=No/2 para t=T, temos
No/2 = No e-k.T
assim
T=Ln(2)/k
Na tabela, apresentamos indicadores de meia-vida de alguns elementos químicos:
| Substância | Meia-vida T |
| Xenônio 133 | 5 dias |
| Bário 140 | 13 dias |
| Chumbo 210 | 22 anos |
| Estrôncio 90 | 25 anos |
| Carbono 14 | 5.568 anos |
| Plutônio | 23.103 anos |
| Urânio 238 | 4.500.000.000 anos |
k = Ln(2)/T = Ln(2)/5568 = 12,3386 por ano
Fonte: AlgoSobre
9.20.2010
Logarítimos
1 - INTRODUÇÃO
O conceito de logaritmo foi introduzido pelo matemático escocês John Napier (1550-1617) e aperfeiçoado pelo inglês Henry Briggs (1561-1630). A descoberta dos logaritmos deveu-se sobretudo à grande necessidade de simplificar os cálculos excessivamente trabalhosos para a época, principalmente na área da astronomia, entre outras. Através dos logaritmos, pode-se transformar as operações de multiplicação em soma, de divisão em subtração, entre outras transformações possíveis, facilitando sobremaneira os cálculos. Na verdade, a idéia de logaritmo é muito simples, e pode-se dizer que o nome logaritmo é uma nova denominação para expoente, conforme veremos a seguir.
Assim, por exemplo, como sabemos que 42 = 16 , onde 4 é a base, 2 o expoente e 16 a potência, na linguagem dos logaritmos, diremos que 2 é o logaritmo de 16 na base 4. Simples, não é?
Nestas condições, escrevemos simbolicamente: log416 = 2.
Outros exemplos:
152 = 225, logo: log15225 = 2
63 = 216, logo: log6216 = 3
54 = 625, logo: log5625 = 4
70 = 1, logo: log71 = 0
2 - DEFINIÇÃO
Dados os números reais b (positivo e diferente de 1), N (positivo) e x , que satisfaçam a relação bx = N, dizemos que x é o logaritmo de N na base b. Isto é expresso simbolicamente da seguinte forma: logbN = x. Neste caso, dizemos que b é a base do sistema de logaritmos, N é o logaritmando ou antilogaritmo e x é o logaritmo.
Exemplos:
a) log28 = 3 porque 23 = 8.
b) log41 = 0 porque 40 = 1.
c) log39 = 2 porque 32 = 9.
d) log55 = 1 porque 51 = 5.
Notas:
1 - quando a base do sistema de logaritmos é igual a 10 , usamos a expressão logaritmo decimal e na representação simbólica escrevemos somente logN ao invés de log10N. Assim é que quando escrevemos logN = x , devemos concluir pelo que foi exposto, que 10x = N.
Existe também um sistema de logaritmos chamado neperiano (em homenagem a John Napier - matemático escocês do século XVI, inventor dos logaritmos), cuja base é o número irracional
e = 2,7183... e indicamos este logaritmo pelo símbolo ln. Assim,
logeM = ln M. Este sistema de logaritmos, também conhecido como sistema de logaritmos naturais, tem grande aplicação no estudo de diversos fenômenos da natureza.
Exemplos:
a) log100 = 2 porque 102 = 100.
b) log1000 = 3 porque 103 = 1000.
c) log2 = 0,3010 porque 100,3010 = 2.
d) log3 = 0,4771 porque 100,4771 = 3.
e) ln e = 1 porque e1 = e = 2,7183...
f) ln 7 = loge7
2 - Os logaritmos decimais (base 10) normalmente são números decimais onde a parte inteira é denominada característica e a parte decimal é denominada mantissa .
Assim por exemplo, sendo log20 = 1,3010, 1 é a característica e 0,3010 a mantissa.
As mantissas dos logaritmos decimais são tabeladas.
Consultando a tábua de logaritmo (qualquer livro de Matemática traz) , podemos escrever por exemplo que log45 = 1,6532. As tábuas de logaritmos decimais foram desenvolvidas por Henry Briggs, matemático inglês do século XVI. Observe que do fato de termos log45 = 1,6532 , podemos concluir pela definição de logaritmo que
101,6532 = 45.
3) Da definição de logaritmo, infere-se (conclui-se) que somente os números reais positivos possuem logaritmo. Assim, não têm sentido as expressões log3(-9) , log20 , etc.
4) É fácil demonstrar as seguintes propriedades imediatas dos logaritmos, todas decorrentes da definição:
P1) O logaritmo da unidade em qualquer base é nulo, ou seja:
logb1 = 0 porque b0 = 1.
P2) O logaritmo da base é sempre igual a 1, ou seja: logbb = 1 , porque b1 = b.
P3) logbbk = k , porque bk = bk .
P4) Se logbM = logbN então podemos concluir que M = N. Esta propriedade é muito utilizada na solução de exercícios envolvendo equações onde aparecem logaritmos (equações logarítmicas).
P5) blogbM = M ou seja: b elevado ao logaritmo de M na base b é igual a M.
3 - PROPRIEDADES OPERATÓRIAS DOS LOGARITMOS
P1 - LOGARITMO DE UM PRODUTO
O logaritmo de um produto é igual a soma dos logaritmos dos fatores, ou seja:
logb(M.N) = logbM + logbN
Exemplo: log20 =log(2.10) = log2 + log10 = 0,3010 + 1 = 1,3010. Observe que como a base não foi especificada, sabemos que ela é igual a 10.
P2 - LOGARITMO DE UM QUOCIENTE
O logaritmo de uma fração ordinária é igual a diferença entre os logaritmos do numerador da fração e do denominador, ou seja:
logb(M/N) = logbM - logbN
Exemplo: log0,02 = log(2/100) = log2 - log100 = 0,3010 - 2,0000 = -1,6990. Do exposto anteriormente, podemos concluir que, sendo log0,02 = -1,6990 então 10-1,6990 = 0,02.
Da mesma forma podemos exemplificar:
log5 = log(10/2) = log10 - log2 = 1 - 0,3010 = 0,6990.
Observação: a não indicação da base, subtende-se logaritmos decimal (base 10).
Nota: Chamamos de cologaritmo de um número positivo N numa base b, ao logaritmo do inverso multiplicativo de N, também na base b. Ou seja:
cologbN = logb(1/N) = logb1 - logbN = 0 - logbN = - logbN.
(menos log de N na base b).
Exemplo: colog10 = -log10 = -1.
P3 - LOGARITMO DE UMA POTENCIA
Temos a seguinte fórmula, facilmente demonstrável: logbMk = k.logbM.
Exemplo: log5256 = 6.log525 = 6.2 = 12.
P4 - MUDANÇA DE BASE
Às vezes, para a solução de problemas, temos necessidade de mudar a base de um sistema de logaritmos, ou seja, conhecemos o logaritmo de N na base b e desejamos obter o logaritmo de N numa base a . Esta mudança de base, muito importante na solução de exercícios, poderá ser feita de acordo com a fórmula a seguir, cuja demonstração não apresenta dificuldades, aplicando-se os conhecimentos aqui expostos.
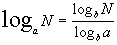
Exemplos:
a) log416 = log216 / log24 (2 = 4:2)
b) log864 = log264 / log28 (2 = 6:3)
c) log25125 = log5125 / log525 = 3 / 2 = 1,5. Temos então que 251,5 = 125.
Notas:
1 - na resolução de problemas, é sempre muito mais conveniente mudar um log de uma base maior para uma base menor, pois isto simplifica os cálculos.
2 - Duas conseqüências importantes da fórmula de mudança de base são as seguintes:
a) logbN = logN / logb (usando a base comum 10, que não precisa ser indicada).
b) logba . logab = 1
Exemplos:
a) log37 . log73 = 1
b) log23 = log3 / log2 = 0,4771 / 0,3010 = 1,5850
4 - A FUNÇÃO LOGARÍTIMICA
Considere a função y = ax , denominada função exponencial, onde a base a é um número positivo e diferente de 1, definida para todo x real.
Observe que nestas condições, ax é um número positivo, para todo x Î R, onde R é o conjunto dos números reais.Denotando o conjunto dos números reais positivos por R+* , poderemos escrever a função exponencial como segue:
f: R ® R+* ; y = ax , 0 < a ¹ 1 Esta função é bijetora, pois:
a) é injetora, ou seja: elementos distintos possuem imagens distintas.
b) É sobrejetora, pois o conjunto imagem coincide com o seu contradomínio.
Assim sendo, a função exponencial é BIJETORA e, portanto, é uma função inversível, OU SEJA, admite uma função inversa.
Vamos determinar a função inversa da função y = ax , onde 0 < a ¹ 1.
Permutando x por y, vem:
x = ay \ y = logaxPortanto, a função logarítmica é então:
f: R+* ® R ; y = logax , 0 < a ¹ 1.Mostramos a seguir, os gráficos das funções exponencial ( y = ax ) e logarítmica
( y = logax ), para os casos a > 1 e 0 < a ¹ 1. Observe que, sendo as funções, inversas, os seus gráficos são curvas simétricas em relação à bissetriz do primeiro e terceiro quadrantes, ou seja, simétricos em relação à reta y = x.
Da simples observação dos gráficos acima, podemos concluir que:
1 - para a > 1, as funções exponencial e logarítmica são CRESCENTES.
2 - para 0 < a ¹ 1, elas são DECRESCENTES.
3 - o domínio da função y = logax é o conjunto R+* .
4 - o conjunto imagem da função y = logax é o conjunto R dos números reais.
5 - o domínio da função y = ax é o conjunto R dos números reais.
6 - o conjunto imagem da função y = ax é o conjunto R+* .
7 - observe que o domínio da função exponencial é igual ao conjunto imagem da função logarítmica e que o domínio da função logarítmica é igual ao conjunto imagem da função exponencial. Isto ocorre porque as funções são inversas entre si. Vamos agora, resolver os seguintes exercícios sobre logaritmos:
1 - Se S é a soma das raízes da equação log2 x - logx - 2 = 0 , então calcule o valor
de 1073 - 10S.
SOLUÇÃO:
Façamos logx = y; vem:
y2 - y - 2 = 0
Resolvendo a equação do segundo grau acima, encontramos: y = 2 ou y = -1.
Portanto,
logx = 2 OU logx = -1
Como a base é igual a 10, teremos:
log10x = 2 \ x = 102 = 100
log10x = -1 \ x = 10-1 = 1/10 As raízes procuradas são, então, 100 e 1/10.
Conforme enunciado do problema, teremos:
S = 100 + 1/10 = 1000/10 + 1/10 = 1001/10
Logo, o valor de 1073 - 10S será:
1073 - 10(1001/10) = 1073 - 1001 = 72
Resp: 72
2 - Calcule o valor de y = 6x onde x = log32 . log63 .
SOLUÇÃO:
Substituindo o valor de x, vem:
y = 6log32 . log63 = (6log63)log32 = 3log32 = 2
Na solução acima, empregamos a propriedade blogbM = M , vista anteriormente.
Resp: 2
3 - UEFS - Sendo log 2 = 0,301, o número de algarismos de 520 é:
a) 13
b) 14
c) 19
d) 20
e) 27
SOLUÇÃO:
Seja n = 520 . Podemos escrever, usando logaritmo decimal:
log n = log 520 = 20.log5
Para calcular o valor do logaritmo decimal de 5, ou seja, log5, basta lembrar que podemos escrever:
log 5 = log (10/2) = log 10 - log 2 = 1 - 0,301 = 0,699
Portanto, log n = 20 . 0,699 = 13,9800
Da teoria vista acima, sabemos que se log n = 13,9800, isto significa que a característica do log decimal vale 13 e, portanto, o número n possui 13 + 1 , ou seja 14 algarismos.
Portanto, a resposta correta é a letra B.
4 - UFBA - Considere a equação 10x + 0,4658 = 368. Sabendo-se que
log 3,68 = 0,5658 , calcule 10x.
SOLUÇÃO:
Temos: 10x + 0,4658 = 368
Daí, podemos escrever:
log 368 = x + 0,4658 \ x = log 368 - 0,4658
Ora, é dado que: log 3,68 = 0,5658, ou seja:
log(368/100) = 0,5658Logo, log 368 - log 100 = 0,5658 \ log 368 - 2 = 0,5658 , já que
log 100 = 2 (pois 102 = 100).
Daí, vem então:
log 368 = 2,5658 Então, x = log 368 - 0,4658 = 2,5658 - 0,4658 = 2,1
Como o problema pede o valor de 10x, vem: 10.2,1 = 21
Resp: 21
5 - Se log N = 2 + log 2 - log 3 - 2log 5 , calcule o valor de 30N.
SOLUÇÃO:
Podemos escrever:
logN = 2 + log2 - log3 - log52
logN = 2 + log2 - log3 - log25
logN = 2 + log2 - (log3 + log25)
Como 2 = log100, fica:
logN = (log100 + log2) - (log3 + log25)
logN = log(100.2) - log(3.25)
logN = log200 - log75
logN = log(200/75)
Logo, concluímos que N = 200/75
Simplificando, fica:
N = 40/15 = 8/3
Logo, 30N = 30(8/3) = 80
Resp: 30N = 80
Agora, resolva estes:
1 - UFBA - Sendo log2 = 0,301 e x = 53 .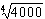
, então o logx é:
*a) 2,997
b) 3,398
c) 3,633
d) 4,398
e) 5,097
2 - UEFS - O produto das raízes da equação log(x2 -7x + 14) = 2log2 é:
01) 5
02) 7
*03) 10
04) 14
05) 35
3 - UCSal - Se 12n+1 = 3n+1 . 8 , então log2 n é igual a:
a) -2
*b) -1
c) 1/2
d) 1
e) 2
4 - UEFS - O domínio da função y = log [(2x-3)/(4-x)] é:
a) (-3/2,4)
b) (-4,3/2)
c) (-4,2)
*d) (3/2,4)
e) (3/2,10)
5 - UFBA - Determine o valor de x que satisfaz à equação log2 (x-3) + log2 (x-2) = 1.
Resp: 4
6 - UFBA - Existe um número x diferente de 10, tal que o dobro do seu logaritmo decimal excede de duas unidades o logaritmo decimal de x-9. Determine x.
Resp: 90
7 - PUC-SP - O logaritmo, em uma base x, do número y = 5 + x/2 é 2. Então x é igual a:
a) 3/2
b) 4/3
c) 2
d)5
*e) 5/2
8 - PUC-SP - Se x+y = 20 e x - y = 5 , então log(x2 - y2 ) é igual a:
a) 100
*b) 2
c) 25
d) 12,5
e) 1000
Sugestão: observe que x2 - y2 = (x - y) (x + y)
Fonte: AlgoSobre
O conceito de logaritmo foi introduzido pelo matemático escocês John Napier (1550-1617) e aperfeiçoado pelo inglês Henry Briggs (1561-1630). A descoberta dos logaritmos deveu-se sobretudo à grande necessidade de simplificar os cálculos excessivamente trabalhosos para a época, principalmente na área da astronomia, entre outras. Através dos logaritmos, pode-se transformar as operações de multiplicação em soma, de divisão em subtração, entre outras transformações possíveis, facilitando sobremaneira os cálculos. Na verdade, a idéia de logaritmo é muito simples, e pode-se dizer que o nome logaritmo é uma nova denominação para expoente, conforme veremos a seguir.
Assim, por exemplo, como sabemos que 42 = 16 , onde 4 é a base, 2 o expoente e 16 a potência, na linguagem dos logaritmos, diremos que 2 é o logaritmo de 16 na base 4. Simples, não é?
Nestas condições, escrevemos simbolicamente: log416 = 2.
Outros exemplos:
152 = 225, logo: log15225 = 2
63 = 216, logo: log6216 = 3
54 = 625, logo: log5625 = 4
70 = 1, logo: log71 = 0
2 - DEFINIÇÃO
Dados os números reais b (positivo e diferente de 1), N (positivo) e x , que satisfaçam a relação bx = N, dizemos que x é o logaritmo de N na base b. Isto é expresso simbolicamente da seguinte forma: logbN = x. Neste caso, dizemos que b é a base do sistema de logaritmos, N é o logaritmando ou antilogaritmo e x é o logaritmo.
Exemplos:
a) log28 = 3 porque 23 = 8.
b) log41 = 0 porque 40 = 1.
c) log39 = 2 porque 32 = 9.
d) log55 = 1 porque 51 = 5.
Notas:
1 - quando a base do sistema de logaritmos é igual a 10 , usamos a expressão logaritmo decimal e na representação simbólica escrevemos somente logN ao invés de log10N. Assim é que quando escrevemos logN = x , devemos concluir pelo que foi exposto, que 10x = N.
Existe também um sistema de logaritmos chamado neperiano (em homenagem a John Napier - matemático escocês do século XVI, inventor dos logaritmos), cuja base é o número irracional
e = 2,7183... e indicamos este logaritmo pelo símbolo ln. Assim,
logeM = ln M. Este sistema de logaritmos, também conhecido como sistema de logaritmos naturais, tem grande aplicação no estudo de diversos fenômenos da natureza.
Exemplos:
a) log100 = 2 porque 102 = 100.
b) log1000 = 3 porque 103 = 1000.
c) log2 = 0,3010 porque 100,3010 = 2.
d) log3 = 0,4771 porque 100,4771 = 3.
e) ln e = 1 porque e1 = e = 2,7183...
f) ln 7 = loge7
2 - Os logaritmos decimais (base 10) normalmente são números decimais onde a parte inteira é denominada característica e a parte decimal é denominada mantissa .
Assim por exemplo, sendo log20 = 1,3010, 1 é a característica e 0,3010 a mantissa.
As mantissas dos logaritmos decimais são tabeladas.
Consultando a tábua de logaritmo (qualquer livro de Matemática traz) , podemos escrever por exemplo que log45 = 1,6532. As tábuas de logaritmos decimais foram desenvolvidas por Henry Briggs, matemático inglês do século XVI. Observe que do fato de termos log45 = 1,6532 , podemos concluir pela definição de logaritmo que
101,6532 = 45.
3) Da definição de logaritmo, infere-se (conclui-se) que somente os números reais positivos possuem logaritmo. Assim, não têm sentido as expressões log3(-9) , log20 , etc.
4) É fácil demonstrar as seguintes propriedades imediatas dos logaritmos, todas decorrentes da definição:
P1) O logaritmo da unidade em qualquer base é nulo, ou seja:
logb1 = 0 porque b0 = 1.
P2) O logaritmo da base é sempre igual a 1, ou seja: logbb = 1 , porque b1 = b.
P3) logbbk = k , porque bk = bk .
P4) Se logbM = logbN então podemos concluir que M = N. Esta propriedade é muito utilizada na solução de exercícios envolvendo equações onde aparecem logaritmos (equações logarítmicas).
P5) blogbM = M ou seja: b elevado ao logaritmo de M na base b é igual a M.
3 - PROPRIEDADES OPERATÓRIAS DOS LOGARITMOS
P1 - LOGARITMO DE UM PRODUTO
O logaritmo de um produto é igual a soma dos logaritmos dos fatores, ou seja:
logb(M.N) = logbM + logbN
Exemplo: log20 =log(2.10) = log2 + log10 = 0,3010 + 1 = 1,3010. Observe que como a base não foi especificada, sabemos que ela é igual a 10.
P2 - LOGARITMO DE UM QUOCIENTE
O logaritmo de uma fração ordinária é igual a diferença entre os logaritmos do numerador da fração e do denominador, ou seja:
logb(M/N) = logbM - logbN
Exemplo: log0,02 = log(2/100) = log2 - log100 = 0,3010 - 2,0000 = -1,6990. Do exposto anteriormente, podemos concluir que, sendo log0,02 = -1,6990 então 10-1,6990 = 0,02.
Da mesma forma podemos exemplificar:
log5 = log(10/2) = log10 - log2 = 1 - 0,3010 = 0,6990.
Observação: a não indicação da base, subtende-se logaritmos decimal (base 10).
Nota: Chamamos de cologaritmo de um número positivo N numa base b, ao logaritmo do inverso multiplicativo de N, também na base b. Ou seja:
cologbN = logb(1/N) = logb1 - logbN = 0 - logbN = - logbN.
(menos log de N na base b).
Exemplo: colog10 = -log10 = -1.
P3 - LOGARITMO DE UMA POTENCIA
Temos a seguinte fórmula, facilmente demonstrável: logbMk = k.logbM.
Exemplo: log5256 = 6.log525 = 6.2 = 12.
P4 - MUDANÇA DE BASE
Às vezes, para a solução de problemas, temos necessidade de mudar a base de um sistema de logaritmos, ou seja, conhecemos o logaritmo de N na base b e desejamos obter o logaritmo de N numa base a . Esta mudança de base, muito importante na solução de exercícios, poderá ser feita de acordo com a fórmula a seguir, cuja demonstração não apresenta dificuldades, aplicando-se os conhecimentos aqui expostos.
Exemplos:
a) log416 = log216 / log24 (2 = 4:2)
b) log864 = log264 / log28 (2 = 6:3)
c) log25125 = log5125 / log525 = 3 / 2 = 1,5. Temos então que 251,5 = 125.
Notas:
1 - na resolução de problemas, é sempre muito mais conveniente mudar um log de uma base maior para uma base menor, pois isto simplifica os cálculos.
2 - Duas conseqüências importantes da fórmula de mudança de base são as seguintes:
a) logbN = logN / logb (usando a base comum 10, que não precisa ser indicada).
b) logba . logab = 1
Exemplos:
a) log37 . log73 = 1
b) log23 = log3 / log2 = 0,4771 / 0,3010 = 1,5850
4 - A FUNÇÃO LOGARÍTIMICA
Considere a função y = ax , denominada função exponencial, onde a base a é um número positivo e diferente de 1, definida para todo x real.
Observe que nestas condições, ax é um número positivo, para todo x Î R, onde R é o conjunto dos números reais.Denotando o conjunto dos números reais positivos por R+* , poderemos escrever a função exponencial como segue:
f: R ® R+* ; y = ax , 0 < a ¹ 1 Esta função é bijetora, pois:
a) é injetora, ou seja: elementos distintos possuem imagens distintas.
b) É sobrejetora, pois o conjunto imagem coincide com o seu contradomínio.
Assim sendo, a função exponencial é BIJETORA e, portanto, é uma função inversível, OU SEJA, admite uma função inversa.
Vamos determinar a função inversa da função y = ax , onde 0 < a ¹ 1.
Permutando x por y, vem:
x = ay \ y = logaxPortanto, a função logarítmica é então:
f: R+* ® R ; y = logax , 0 < a ¹ 1.Mostramos a seguir, os gráficos das funções exponencial ( y = ax ) e logarítmica
( y = logax ), para os casos a > 1 e 0 < a ¹ 1. Observe que, sendo as funções, inversas, os seus gráficos são curvas simétricas em relação à bissetriz do primeiro e terceiro quadrantes, ou seja, simétricos em relação à reta y = x.
Da simples observação dos gráficos acima, podemos concluir que:
1 - para a > 1, as funções exponencial e logarítmica são CRESCENTES.
2 - para 0 < a ¹ 1, elas são DECRESCENTES.
3 - o domínio da função y = logax é o conjunto R+* .
4 - o conjunto imagem da função y = logax é o conjunto R dos números reais.
5 - o domínio da função y = ax é o conjunto R dos números reais.
6 - o conjunto imagem da função y = ax é o conjunto R+* .
7 - observe que o domínio da função exponencial é igual ao conjunto imagem da função logarítmica e que o domínio da função logarítmica é igual ao conjunto imagem da função exponencial. Isto ocorre porque as funções são inversas entre si. Vamos agora, resolver os seguintes exercícios sobre logaritmos:
1 - Se S é a soma das raízes da equação log2 x - logx - 2 = 0 , então calcule o valor
de 1073 - 10S.
SOLUÇÃO:
Façamos logx = y; vem:
y2 - y - 2 = 0
Resolvendo a equação do segundo grau acima, encontramos: y = 2 ou y = -1.
Portanto,
logx = 2 OU logx = -1
Como a base é igual a 10, teremos:
log10x = 2 \ x = 102 = 100
log10x = -1 \ x = 10-1 = 1/10 As raízes procuradas são, então, 100 e 1/10.
Conforme enunciado do problema, teremos:
S = 100 + 1/10 = 1000/10 + 1/10 = 1001/10
Logo, o valor de 1073 - 10S será:
1073 - 10(1001/10) = 1073 - 1001 = 72
Resp: 72
2 - Calcule o valor de y = 6x onde x = log32 . log63 .
SOLUÇÃO:
Substituindo o valor de x, vem:
y = 6log32 . log63 = (6log63)log32 = 3log32 = 2
Na solução acima, empregamos a propriedade blogbM = M , vista anteriormente.
Resp: 2
3 - UEFS - Sendo log 2 = 0,301, o número de algarismos de 520 é:
a) 13
b) 14
c) 19
d) 20
e) 27
SOLUÇÃO:
Seja n = 520 . Podemos escrever, usando logaritmo decimal:
log n = log 520 = 20.log5
Para calcular o valor do logaritmo decimal de 5, ou seja, log5, basta lembrar que podemos escrever:
log 5 = log (10/2) = log 10 - log 2 = 1 - 0,301 = 0,699
Portanto, log n = 20 . 0,699 = 13,9800
Da teoria vista acima, sabemos que se log n = 13,9800, isto significa que a característica do log decimal vale 13 e, portanto, o número n possui 13 + 1 , ou seja 14 algarismos.
Portanto, a resposta correta é a letra B.
4 - UFBA - Considere a equação 10x + 0,4658 = 368. Sabendo-se que
log 3,68 = 0,5658 , calcule 10x.
SOLUÇÃO:
Temos: 10x + 0,4658 = 368
Daí, podemos escrever:
log 368 = x + 0,4658 \ x = log 368 - 0,4658
Ora, é dado que: log 3,68 = 0,5658, ou seja:
log(368/100) = 0,5658Logo, log 368 - log 100 = 0,5658 \ log 368 - 2 = 0,5658 , já que
log 100 = 2 (pois 102 = 100).
Daí, vem então:
log 368 = 2,5658 Então, x = log 368 - 0,4658 = 2,5658 - 0,4658 = 2,1
Como o problema pede o valor de 10x, vem: 10.2,1 = 21
Resp: 21
5 - Se log N = 2 + log 2 - log 3 - 2log 5 , calcule o valor de 30N.
SOLUÇÃO:
Podemos escrever:
logN = 2 + log2 - log3 - log52
logN = 2 + log2 - log3 - log25
logN = 2 + log2 - (log3 + log25)
Como 2 = log100, fica:
logN = (log100 + log2) - (log3 + log25)
logN = log(100.2) - log(3.25)
logN = log200 - log75
logN = log(200/75)
Logo, concluímos que N = 200/75
Simplificando, fica:
N = 40/15 = 8/3
Logo, 30N = 30(8/3) = 80
Resp: 30N = 80
Agora, resolva estes:
1 - UFBA - Sendo log2 = 0,301 e x = 53 .
, então o logx é:*a) 2,997
b) 3,398
c) 3,633
d) 4,398
e) 5,097
2 - UEFS - O produto das raízes da equação log(x2 -7x + 14) = 2log2 é:
01) 5
02) 7
*03) 10
04) 14
05) 35
3 - UCSal - Se 12n+1 = 3n+1 . 8 , então log2 n é igual a:
a) -2
*b) -1
c) 1/2
d) 1
e) 2
4 - UEFS - O domínio da função y = log [(2x-3)/(4-x)] é:
a) (-3/2,4)
b) (-4,3/2)
c) (-4,2)
*d) (3/2,4)
e) (3/2,10)
5 - UFBA - Determine o valor de x que satisfaz à equação log2 (x-3) + log2 (x-2) = 1.
Resp: 4
6 - UFBA - Existe um número x diferente de 10, tal que o dobro do seu logaritmo decimal excede de duas unidades o logaritmo decimal de x-9. Determine x.
Resp: 90
7 - PUC-SP - O logaritmo, em uma base x, do número y = 5 + x/2 é 2. Então x é igual a:
a) 3/2
b) 4/3
c) 2
d)5
*e) 5/2
8 - PUC-SP - Se x+y = 20 e x - y = 5 , então log(x2 - y2 ) é igual a:
a) 100
*b) 2
c) 25
d) 12,5
e) 1000
Sugestão: observe que x2 - y2 = (x - y) (x + y)
Fonte: AlgoSobre
Assinar:
Postagens (Atom)